APIO2013 TASKSAUTHOR
简要题意
给你一些代码,每个数据要求构造一组数据,使其中一个代码AC,另一个代码TLE。
每个代码内部有一个计数器counter,如果counter>1000000则认为TLE,否则认为AC
互相伤害真开心
题解
Subtask1
用Dijkstra干Floyd。
由于Floyd 计数器的值为\(n^3\),和询问和边数无关,所以直接101个点0条边1组询问就可以了(因为询问次数>=1)
数字个数为105(1+101+1+2)
Subtask2
用Floyd干BellmanFord。
注意到它的BellmanFord会在已经得到从源点到所有点的答案后结束。
计数器的值就为 (原点到所有点的最短路长度的最大值\(\times\)E)
那么我们就让最短路长度=v-1。
但是它的更新是按照点从0..v-1对每个点的出边进行松弛。
如果这条最短路从0到v-1就会一遍松弛结束。
所以这条最短路就得反着来。
先连n-1条边权为-1的边:n-1 到 n-2 到n-3...到0.
然后当总边数是E的时候counter就是\((V-1)E\)
由于有总数字个数限制,所以得控制好点数和边数使得恰好卡掉BellmanFord。
显然k组一样的询问会让counter乘k,那就放10组数据。(最多10组)
每组的查询显然是n-1到0的最短路。
当n=98的时候1051条边恰好2222个数字也能卡掉BellmanFord并且让Floyd过。
数据生成器:
vector<pair<int,int> > e[128];
int main(){
freopen("tasksauthor2.out","w",stdout);
int n=98;
printf("%d\n",n);
for(int i=n-1;i;--i)e[i].push_back(make_pair(i-1,-1));
for(int i=1;i<=954;++i)e[rand()%n].push_back(make_pair(rand()%n,rand()%1000000));
for(int i=0;i<n;++i){
printf("%d",e[i].size());
for(auto x:e[i])printf(" %d %d",x.first,x.second);
putchar('\n');
}
printf("%d\n",10);
for(int i=0;i<10;++i)printf("%d %d\n",n-1,0);
return 0;
}Subtask3
用BellmanFord干Floyd,直接用Subtask1的数据即可。
Subtask4
用Floyd干Dijkstra。
Dijkstra每次取出优先队列队首时counter+1。
可以有负边!
第一想法:用负权环让它在圈内打转。
但是要求不能有负权环。
还有另一个办法:让一个点重复被更新多次。
由于Dijkstra是贪心,我们可以让它先沿一个错误的路径瞎走,然后再用一个“初步看上去不是更优秀的”路径再更新一遍。
类似于
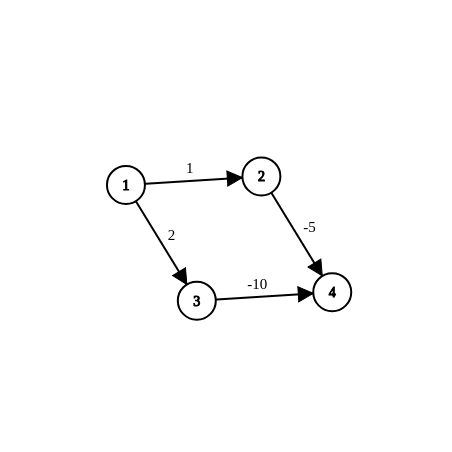
把这样的4个点叫做一组。
然后就会根据贪心,先从1走到2,自然的走到4,从4开始继续更新,然后后面的更新完了再从1到3 ,走到4,再更新
然后4号再去作为1得到另一组。以此类推。
然后越往前的组,负边要指数级增加 类似于5,10 10,20 20,40这样。
然后如果46个点这样就能卡掉Dijkstra了。
但是有188个数字只能拿到14分。
发现点2是没用的 。
稍加修改:
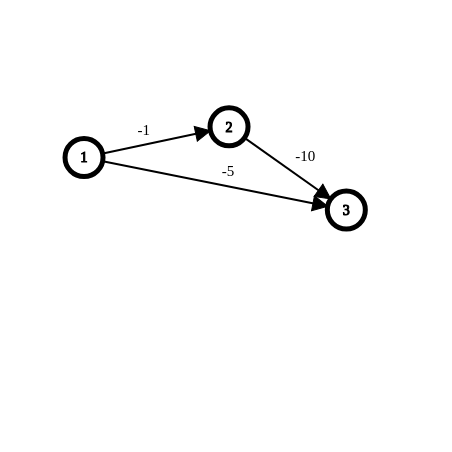
然后3继续作为后面一组的1。
负边依然是从后往前指数级增加。
一共33个点刚好干掉。
Subtask5
用Dijkstra干BellmanFord。
由于数字个数不多,所以可以通过增加点数的方法卡。
点数300,边数340就卡掉了。
vector<pair<int,int> > e[355];
int main(){
freopen("tasksauthor5.out","w",stdout);
int n=300;
printf("%d\n",n);
for(int i=n-1;i;--i)e[i].push_back(make_pair(i-1,-1));
for(int i=1;i<=40;++i)e[0].push_back(make_pair(rand()%n,rand()%1000000));
for(int i=0;i<n;++i){
printf("%d",e[i].size());
for(auto x:e[i])printf(" %d %d",x.first,x.second);
putchar('\n');
}
printf("%d\n",10);
for(int i=0;i<10;++i)printf("%d %d\n",n-1,0);
return 0;
}
Subtask6
用BellmanFord卡Dijkstra。
和Subtask4一样,只是限制更紧了。
发现Dijkstra在第六组询问的时候就挂了,就把询问次数改成6。
(第四组也可以改)
4和6:
#define x first
#define y second
typedef pair<int,int> pii;
vector<pii> e[66];
int main(){
freopen("tasksauthor4.out","w",stdout);
int n=33,k=-1;
for(int i=n-3;i>=0;i-=2){
e[i].push_back(make_pair(i+1,k));
e[i].push_back(make_pair(i+2,2*k));
e[i+1].push_back(make_pair(i+2,2*k));
k=k*2;
}
printf("%d\n",n);
for(int i=0;i<n;++i){
printf("%d",e[i].size());
for(auto x:e[i])printf(" %d %d",x.x,x.y);
putchar('\n');
}
int m=6;
printf("%d\n",m);
for(int i=1;i<=m;++i)printf("%d %d\n",0,n-1);
return 0;
}
Subtask7
问题2。
边数至少1501,点数至少71,至多999。
限制3004,也就是点数随便,边数只能1501。
用恒过器干这个算法,也就是让它TLE。
直接随机一组数据即可如果你随机的数据能不TLE那么恭喜你中奖了
Subtask8
限制还是3004。
用这个算法干恒挂器,也就是让它不TLE。
大力随机多组数据就可以了
如果随机出来的那么恭喜你中奖了
观察代码:
答案从2到v用DFS判断是否可行,可行就结束。
所以需要尽量减少它DFS的次数。
答案是2需要是链或偶环,1501条边显然不可能。
那就让答案是3并且可以很显然的找到答案且让答案2很快的判断是不可行的。
999个点,如果每个点的颜色为1 2 3 1 2 3 1 2 3 1 2 3...。
那么可以先连出一条链1-2-3-4-5-6-7-8-9-...-999,然后再1-3-5-7-9-...-999 2-4-6-8-10-...-998,然后把多余的边从后往前删去即可。
这样答案是3就很轻松的找到,答案是2在第3个点的时候就gg了。
from random import *
import sys
sys.stdout=open("my.out","w")
v=999
e=1501
print(v,e)
for i in range(v-1):
print(i,i+1)
for i in range(503):
print(i,i+2)
并不顺利地获得100分!