各类莫队讲解+ WC2013-糖果公园
这是一篇讲解莫队以及这个题的文章。
1. 莫队
有一些区间询问问题,当得到了[l,r]的答案时,可以O(1)的得到[l,r-1],[l,r+1],[l-1,r],[l+1,r]的答案。
对于这种问题,我们有一种很显然的通过移动l,r指针的暴力。
但是这样面对[1,1],[n,n]循环的数据,会卡到O(qn) 的最坏复杂度。 怎么办呢?
这个莫队算法,就是莫涛队长想出来的优化。
首先把区间按照L/s分块,其中s是块大小。
就是把询问按照L/s从小到大排序,如果相等按R排序。
接下来用上面那个暴力。
时间复杂度为\(O(qs+\frac{n^2}{s})\)
根号平衡得到\(s=\frac{n}{\sqrt{m}}\)时取到最小值\(O(n\sqrt{m})\)
lxl:实际应用的时候\(s=\frac{n}{\sqrt{1.5m}}\)常数最优。
2.带修改莫队
这里的修改是指单点修改。
记录t为当前是第几次修改后。
排序以后也可以t指针也可以\(O(1)\)移动。
还是分块,设块大小为s,按照左端点块编号-右端点块编号-t 三关键字排序,
然后移动3个指针。
时间复杂度\(O(ns+\frac{n^3}{s^2})\)
当\(s=n^\frac{2}{3}\)时取到最小值\(O(n^\frac{5}{3})\)
常数同样优秀。
3.树上莫队
也就是询问树上一条链的答案。
首先对树进行DFS,每个点入一个时间戳,出一个时间戳。得到每个点入和出的时间戳(in[i],out[i]),以及第i个时间戳是哪个点。
例如:
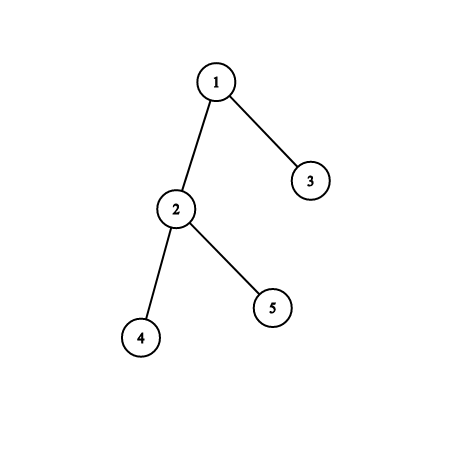
从1开始DFS,得到的时间戳是:in=[1,2,8,3,5],out=[10,7,9,4,6],标记顺序是[1,2,4,4,5,5,2,3,3,1]
我们定义,一个询问[l,r]表示询问所有 l到r这一段标记里,恰好出现了一次的节点的答案。
比如[1,5]就是询问\(1-2-5\)这条路径的答案。
当u和v是同节点,则询问[in[u],in[u]]就可以了。
当v在u的子树里面,我们就可以询问[in[u],in[v]]区间,可以发现不在这条路径上的一定出现了0/2次,在这条路径上的一定出现了1次。
u在v子树中就相反。
否则,显然[in[u],out[u]],[in[v],out[v]]不相交。
假设out[u]<in[v],那么我们可以询问[out[u],in[v]]。此时除了LCA以外,这条路径上的节点恰好出现了一次。
再加上LCA的贡献就可以了。
否则就询问[out[v],in[u]]即可。
4. 树上带修改莫队
就是2+3.
WC 2013 糖果公园(代码)
这题是个树上带修改莫队。
代码:
/*
Author: CNYALI_LK
LANG: C++
PROG: luogu4074.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef long long ll;
typedef pair<ll,ll> pii;
template<class T>ll chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>ll chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
ll read(){
ll s=0,base=1;
char c;
while(!isdigit(c=getchar()))if(c=='-')base=-base;
while(isdigit(c)){s=s*10+(c^48);c=getchar();}
return s*base;
}
char WritellBuffer[1024];
template<class T>void write(T a,char end){
ll cnt=0,fu=1;
if(a<0){putchar('-');fu=-1;}
do{WritellBuffer[++cnt]=fu*(a%10)+'0';a/=10;}while(a);
while(cnt){putchar(WritellBuffer[cnt]);--cnt;}
putchar(end);
}
ll in[102424],out[102424],is[204848],t,dep[102424];
ll to[233333],lst[204847],beg[102423],e;
ll fa[102424][20];
void dfs(ll x,ll f){
fa[x][0]=f;
dep[x]=dep[f]+1;
for(ll i=1;i<20;++i)fa[x][i]=fa[fa[x][i-1]][i-1];
is[in[x]=++t]=x;
for(ll i=beg[x];i;i=lst[i])if(to[i]!=f){
dfs(to[i],x);
}
is[out[x]=++t]=x;
}
void add(ll u,ll v){
to[++e]=v;
lst[e]=beg[u];
beg[u]=e;
/*------------------------*/
to[++e]=u;
lst[e]=beg[v];
beg[v]=e;
}
ll block;
struct _ask{
ll l,r,id,lb,_add,T,rb;
};
_ask ask[102424];
ll lca(ll u,ll v){
if(dep[u]<dep[v])swap(u,v);
for(ll i=19;~i;--i)if(dep[u]-(1<<i)>=dep[v]){
u=fa[u][i];
}
for(ll i=19;~i;--i)if(fa[u][i]!=fa[v][i]){u=fa[u][i];v=fa[v][i];}
if(u!=v){
u=fa[u][0];v=fa[v][0];
}
return u;
}
ll cmp(_ask a,_ask b){return a.lb<b.lb||a.lb==b.lb&&a.rb<b.rb||a.lb==b.lb&&a.rb==b.rb&&a.T<b.T;}
ll _is[102424],cnt[102424],tot,ans[102424];
ll V[102424],w[102424],c[102424];
void ds(ll x){
if(_is[x]){
tot-=w[cnt[c[x]]]*V[c[x]];
--cnt[c[x]];
}
else{
tot+=w[++cnt[c[x]]]*V[c[x]];
}
_is[x]^=1;
}
ll cTo[102424],cFr[102424],pt[102424];
void rem(ll x){
if(_is[pt[x]]){
ds(pt[x]);
c[pt[x]]=cFr[x];
ds(pt[x]);
}
else
c[pt[x]]=cFr[x];
}
void add(ll x){
if(_is[pt[x]]){
ds(pt[x]);
c[pt[x]]=cTo[x];
ds(pt[x]);
}
else
c[pt[x]]=cTo[x];
}
int main(){
#ifdef cnyali_lk
freopen("luogu4074.in","r",stdin);
freopen("luogu4074.out","w",stdout);
#endif
ll n=read(),m=read(),q=0,u,v,_q=read();
for(ll i=1;i<=m;++i)V[i]=read();
for(ll i=1;i<=n;++i)w[i]=read();
for(ll i=1;i<n;++i){
add(read(),read());
}
dfs(1,0);
// for(ll i=1;i<=t;++i)printf("%lld%c",is[i],i==t?'\n':',');
block=(ll)ceil(pow(t,2./3));
for(ll i=1;i<=n;++i)c[i]=read();
ll T=0;
for(ll i=1;i<=_q;++i){
if(!read()){
pt[++T]=read();
cFr[T]=c[pt[T]];
cTo[T]=read();
c[pt[T]]=cTo[T];
}
else{
ask[++q].id=q;
ask[q].T=T;
u=read();v=read();
if(u==v){
ask[q].lb=ask[q].rb=(ask[q].l=ask[q].r=in[u])/block;
ask[q]._add=0;
}
else
if(in[u]<in[v]&&out[v]<out[u]){
ask[q].lb=(ask[q].l=in[u])/block;
ask[q].rb=(ask[q].r=in[v])/block;
ask[q]._add=0;
}
else if(in[u]>in[v]&&out[v]>out[u]){
ask[q].lb=(ask[q].l=in[v])/block;
ask[q].rb=(ask[q].r=in[u])/block;
ask[q]._add=0;
}
else{
if(out[u]>in[v]){
swap(u,v);
}
ask[q].lb=(ask[q].l=out[u])/block;
ask[q].rb=(ask[q].r=in[v])/block;
ask[q]._add=lca(u,v);
}
}
}
// for(ll i=1;i<=q;++i)printf("%lld %lld %lld %lld\n",ask[i].l,ask[i].r,ask[i].T,ask[i]._add);
sort(ask+1,ask+q+1,cmp);
ll l=1,r=t;
for(ll i=1;i<=q;++i){
while(T>ask[i].T){ rem(T);--T; }
while(T<ask[i].T){ add(++T); }
while(l<ask[i].l){
ds(is[l]);
++l;
}
while(l>ask[i].l){
ds(is[--l]);
}
while(r>ask[i].r){
ds(is[r]);
--r;
}
while(r<ask[i].r){
ds(is[++r]);
}
if(ask[i]._add)ds(ask[i]._add);
ans[ask[i].id]=tot;
if(ask[i]._add)ds(ask[i]._add);
}
for(ll i=1;i<=q;++i)printf("%lld\n",ans[i]);
return 0;
}