后缀自动机学习笔记
参考了hihoCoder上的内容..题目也都是hihoCoder的。
什么是SAM
对于一个字符串S,它对应的后缀自动机(Suffix Automaton,简称SAM)是一个最小的确定有限状态自动机(DFA),接受且只接受S的后缀。
比如对于字符串S="aabbabd",它的后缀自动机是:
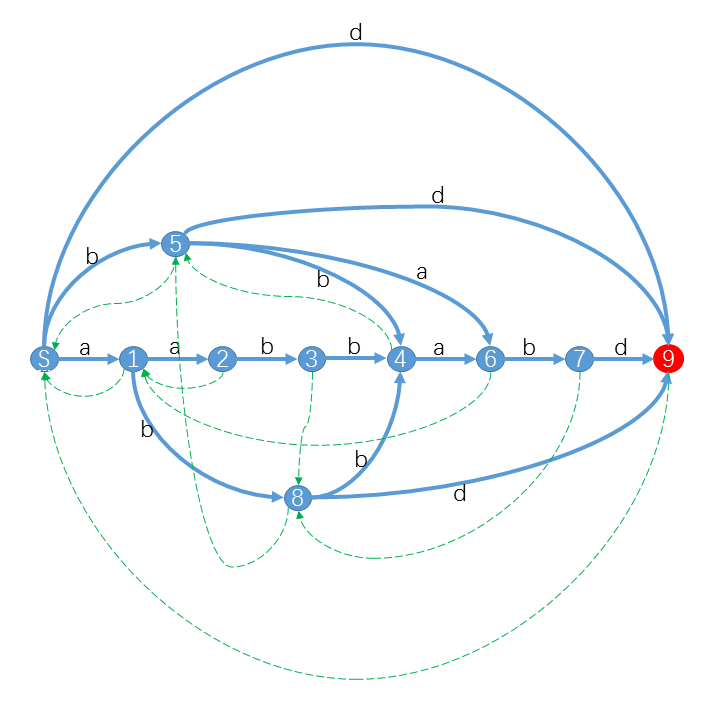
其中红色状态是终结状态。你可以发现对于S的后缀,我们都可以从S出发沿着字符标示的路径(蓝色实线)转移,最终到达终结状态。例如"bd"对应的路径是S59,"abd"对应的路径是S189,"abbabd"对应的路径是S184679。而对于不是S后缀的字符串,你会发现从S出发,最后会到达非终结状态或者“无路可走”。特别的,对于S的子串,最终会到达一个合法状态。例如"abba"路径是S1846,"bbab"路径是S5467。而对于其他不是S子串的字符串,最终会“无路可走”。 例如"aba"对应S18X,"aaba"对应S123X。(X表示没有转移匹配该字符)
endpos
定义endpos(s)表示s在S中每次出现的结束位置集合。
可以发现,设|s_1|≤|s_2|,则endpos(s_2) ⊆ endpos(s_1)当且仅当s_1是s_2的后缀,否则显然endpos(s_1) ∩ endpos(s_2)=∅。
所以每个endpos(s)集合对应的s一定是一个串的一些连续后缀。
我们把endpos相同的s用同一个状态st表示,设maxlen(st),minlen(st)表示s长度的最大值和最小值,longest(st)表示最长的s,substr(st)表示s构成的集合。
Suffix Links
Suffix Links就是上图中的绿色虚线。
substr(st)表示longest(st)的一些连续后缀,会在长度minlen(st)的地方断掉。而长度=minlen(st)-1的后缀会被分到另一个状态st',令link(st)=st'。
一个状态st沿着Suffix
Links一直走,substr(st)并集刚好就是longest(st)的所有后缀。
Transition Function
对于endpos(s)相同的s,endpos(s+c)一定也相同(其中c是同一个字符)
定义trans(st,c)=x|longest(st)+c∈x
怎么构造SAM
SAM可以通过\(O(|S|)\)的增量法构造。
#### 精简定义的状态
minlen(st)可以通过maxlen(link(st))+1得到。
若知道endpos(st)中任意一个位置,则longest(st),substr(st)都可以通过maxlen(st)算出。
所以这三个都不用记。
具体构造方法
namespace SAM{
int to[2000005][26],fail[2000005],len[2000005],t=1,now=1;
void extend(int w){
int nx=++t;
len[nx]=len[now]+1;
int i=now;
for(;i&&!to[i][w];i=fail[i])to[i][w]=nx;//1
if(!i){//2
fail[nx]=1;
}
else if(len[to[i][w]]==len[i]+1){//3
fail[nx]=to[i][w];
}
else{//4
int a=++t,b=to[i][w];
len[a]=len[i]+1;
for(int j=0;j<26;++j)to[a][j]=to[b][j];
fail[a]=fail[b];
fail[b]=fail[nx]=a;
for(;i&&to[i][w]==b;i=fail[i])to[i][w]=a;
}
now=nx;
}
ll calc(){
ll s=0;
for(int i=1;i<=t;++i)s+=len[i]-len[fail[i]];
return s;
}
}代码解释?:
fail[x]=trans(x), to[x][y]=trans(x,y),len[x]=maxlen(x) k,
假设我们得到了S的SAM,trans(start,S)=st',要在S之后加个c。
首先新建状态t。代表endpos(st)={|S|+1}`.
- 由于
i表示的所有串s都满足s+c没出现过,所以endpos(s+c)={|S|+1}。 - 由于
S的所有后缀s都满足s+c没出现过,所以显然minlen(st)=1 longest(trans(i,c))=longest(i)+c,由于longest(i)是longest(st')的后缀,longest(trans(i,c))也是longest(st)的后缀。所以link(st)可以直接=trans(i,c)longest(i)+c是old=longest(trans(i,c))和longest(st)的后缀,endpos(longest(i)+c)显然和endpos(trans(i,c)),endpos(st)都不一样,所以要另开一个节点new。由于原来的longest(link(old))是longest(new)的后缀,所以link(new)就是原来的link(old)。link(old),link(st)显然都是new。由于new是从old拆分出来的,trans(new,x)的初值就是trans(old,w)。显然对于i沿着link走所有满足trans(i,c)=old的都可以改成trans(i,c)=new。
应用
求一个字符串不同子串个数
就是sum(maxlen(st)-minlen(st)+1)=sum(maxlen(st)-maxlen(link(st))),当然也可以直接在DAG上DP
#### 求S在T中出现次数
就是求T的SAM中endpos(S)的大小。
显然Suffix Links构成了一个以start为根的树。
对于T的每一个前缀T[1:i],可以表示这个前缀的状态到start上路径的所有状态endpos都要加上i。
当然也可以通过树上差分解决:每次新建st的时候cnt(st)=0,复制出new的时候cnt(new)=0,最后树上前缀和一下。
求S中长度为k的串出现次数最大值f[k]。
对于每个st,显然chkmax(f[i],cnt(st))for all i≤maxlen(st)
所以可以chkmax(f[maxlen(st)],cnt(st))然后后缀max一下
namespace SAM{
int to[2000005][26],len[2000005],fail[2000005],t=1,now=1,cnt[2000005],l,is[2000005];
void extend(int w){
int nx=++t;
len[nx]=++l;
is[nx]=1;
int i=now;
for(;i && !to[i][w];i=fail[i])to[i][w]=nx;
if(!i)fail[nx]=1;
else if(len[i]+1==len[to[i][w]]){
fail[nx]=to[i][w];
}
else{
int nw=++t,o=to[i][w];
len[nw]=len[i]+1;
fail[nw]=fail[o];
for(int j=0;j<26;++j)to[nw][j]=to[o][j];
fail[o]=fail[nx]=nw;
for(;i&&to[i][w]==o;i=fail[i])to[i][w]=nw;
}
now=nx;
}
int a[1000005],b[2000005],mx[1000005];
void work(){
for(int i=0;i<=l;++i)a[i]=0;
for(int i=1;i<=t;++i)++a[len[i]],cnt[i]=is[i];
for(int i=1;i<=l;++i)a[i]+=a[i-1];
for(int i=t;i;--i){b[a[len[i]]]=i;--a[len[i]];}
for(int i=t;i;--i){
cnt[fail[b[i]]]+=cnt[b[i]];
chkmax(mx[len[b[i]]],cnt[b[i]]);
}
for(int i=l;i;--i)chkmax(mx[i-1],mx[i]);
for(int i=1;i<=l;++i)write(mx[i],'\n');
}
}对S建后缀自动机。然后对T的每个前缀求最长匹配的后缀长度。
假设已经求出了T的答案要求出T+c的答案。
设当前匹配到的状态是st,匹配的长度是l。
进行操作: 1.
若trans(st,c)存在,则st=trans(st,c),l=l+1。 2.
否则l=maxlen(link(st)),st=link(st),回到1
求S有多少个子串和T循环同构。
如果S多组询问:
对T+T建SAM,然后求出S每个前缀S[1:i]最长匹配后缀长度长度。若≥|T|,则ans=ans+1
如果T多组询问:
对S建SAM,然后求出T+T每个前缀匹配到的位置。
若匹配到某个前缀时st满足maxlen(link(st))≥|T|则st=link(st)没有问题。若l≥|T|,则若没到达过这个st(就是这个串没出现过)则ans+=cnt(st)(求出这个串在S中出现次数)
int match(char *t){
++ts;
int at=1,s=0,ans=0;
int m=strlen(t);
for(char *c=t;*c;++c){
int w=*c-'a';
while(at && !to[at][w])at=fail[at];
if(!at){at=1;s=0;}
else{s=min(s,len[at])+1;at=to[at][w];}
}
for(char *c=t;*c;++c){
int w=*c-'a';
while(at && !to[at][w])at=fail[at];
if(!at){at=1;s=0;}
else{s=min(s,len[at])+1;at=to[at][w];}
while(len[fail[at]]>=m){at=fail[at];s=len[at];}
if(s>=m && tag[at]!=ts){
ans+=cnt[at];
tag[at]=ts;
}
}
return ans;
}