分离丧失的既视感
神仙题。
题意
有n个区间\([l_i,r_i]\),你需要选出一些区间,使得:
如果把每个区间当成一个点,把相交的区间对应的点连边,那么这些区间形成了一颗树。
\(n\le 2000\)
题解
注意到满足条件的区间一定是外层的“大区间”依次相交内层可能含有互不接触的“小区间”。
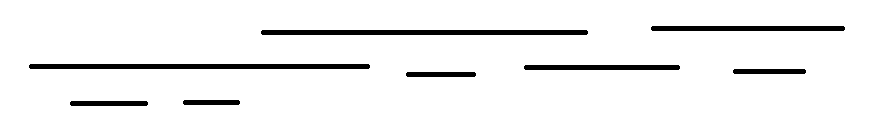
先把区间按照左端点排序。
设\(dp_{i,j}\)表示已经考虑了前i-1个区间,区间最右端点是j的方案数。设\(nxt_i\)是左端点\(>i\)的第一个区间(没有就是n+1)。
从前往后转移。
区间i不选择:右端点不会变,下一个考虑的是i+1。\(dp_{i+1,j}+=dp_{i,j}\)。
区间i选择(能放进去,并且是小区间,由于\(l_i,r_i\)区间就会覆盖两次,那么下一个可以选择的区间必须左端点\(>r_i\),所以\(dp_{nxt_{ri},j}+=dp_{i,j}\)。
(能放进去的情况下)区间i是大区间,由于\(l_i,j\)区间就会覆盖两次,下一个选择的区间左端点必须\(> j\)。同时总共的右端点就会变成\(r_i\),所以\(dp_{nxt_j,r_i}+=dp_{i,j}\)。
特别的,对于第一个放i区间的情况,\(dp_{i+1,r_i}+=1\)。
那么答案就是\(\sum\limits_i dp_{n+1,i}\)
/*
Author: CNYALI_LK
LANG: C++
PROG: b.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
#define x first
#define y second
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef long long ll;
typedef pair<int,int> pii;
template<class T>int chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>int chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
template<class T>int dcmp(T a,T b){return a>b;}
template<int *a>int cmp_a(int x,int y){return a[x]<a[y];}
#define min mmin
#define max mmax
#define abs aabs
int read(){
int s=0,base=1;
char c;
while(!isdigit(c=getchar()))if(c=='-')base=-base;
while(isdigit(c)){s=s*10+(c^48);c=getchar();}
return s*base;
}
int f[2047][4095],nxt[4095];
const int p=1000000007;
pii a[2047];
void Add(int &x,int y){if((x+=y)>=p)x-=p;}
int main(){
#ifdef cnyali_lk
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
#endif
int n;
n=read();
for(int i=1;i<=n;++i){
a[i].x=read();a[i].y=read();
}
sort(a+1,a+n+1);
a[n+1].x=19260817;
for(int i=1,j=1;i<=4000;nxt[i]=j,++i)while(a[j].x<=i)++j;
for(int i=1;i<=n;++i){
Add(f[i+1][a[i].y],1);
for(int j=1;j<=4000;++j)if(f[i][j]){
Add(f[i+1][j],f[i][j]);
if(j>=a[i].x){
if(a[i].y<=j){
Add(f[nxt[a[i].y]][j],f[i][j]);
}
else Add(f[nxt[j]][a[i].y],f[i][j]);
}
}
}
int ans=0;
for(int i=1;i<=4000;++i)Add(ans,f[n+1][i]);
printf("%d\n",ans);
return 0;
}