浴谷八连测R3 题解

A

分类讨论直接前缀和搞搞。

/*
Author: CNYALI_LK
LANG: C++
PROG: a.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
#define x first
#define y second
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef long long ll;
typedef pair<ll,ll> pii;
template<class T>ll chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>ll chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
ll read(){
    ll s=0,base=1;
    char c;
    while(!isdigit(c=getchar()))if(c=='-')base=-base;
    while(isdigit(c)){s=s*10+(c^48);c=getchar();}
    return s*base;
}
const ll p=19260817;
ll dis[204847],fdis[204847],tdis[204847];
ll w[204847],fw[204847],tw[204847],qw[204847];
int main(){
#ifdef cnyali_lk
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
#endif
    ll n,m,x,l,r;
    n=read();
    m=read();
    for(ll i=1;i<n;++i)dis[i]=read()%p;
    for(ll i=1;i<=n;++i){
        w[i]=read()%p;
        qw[i]=(qw[i-1]+w[i])%p;
    }
    for(ll i=2;i<=n;++i){
        fdis[i]=(dis[i-1]+fdis[i-1])%p;
        fw[i]=(fw[i-1]+fdis[i]*w[i])%p;
    }
    for(ll i=n-1;i;--i){
        tdis[i]=(tdis[i+1]+dis[i])%p;
        tw[i]=(tw[i+1]+tdis[i]*w[i])%p;
    }
    for(;m;--m){
        x=read();l=read();r=read(); 
        if(x<l){
            printf("%lld\n",(fw[r]-fw[l-1]+p-fdis[x]*(qw[r]-qw[l-1]+p)%p+p)%p);
        }
        else if(r<x){
            printf("%lld\n",(tw[l]-tw[r+1]+p-tdis[x]*(qw[r]-qw[l-1]+p)%p+p)%p);
        }
        else{
            printf("%lld\n",((fw[r]-fw[x]+p-fdis[x]*(qw[r]-qw[x])%p+p)+(tw[l]-tw[x]+p-tdis[x]*(qw[x-1]-qw[l-1])%p+p))%p);
        }
    }
    return 0;
}

B

首先显然两部分的区域在各行格列是连续的。类似于这样：

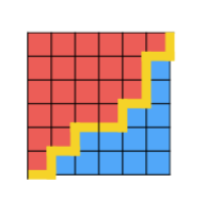
然后每一行的轮廓线是单调的。

设最大值为Mx,最小值为Mn。

对于答案k，满足一部分$\ge Mx-k$（假设为红色），另一部分$\le Mn+k$（假设为蓝色）。

红色可能在左上右上左下右下。

那么就可以通过将这个矩阵旋转90°多次（0,1,2,3次），来使得红色在左上。

二分答案k，贪心的计算红色，判断蓝色是否满足$\le Mn+k$。

时间复杂度$O(nm\log A)$ A是元素大小。

/*
Author: CNYALI_LK
LANG: C++
PROG: b.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %lld\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
#define x first
#define y second
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef long long ll;
typedef pair<ll,ll> pii;
template<class T>ll chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>ll chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
ll read(){
    ll s=0,base=1;
    char c;
    while(!isdigit(c=getchar()))if(c=='-')base=-base;
    while(isdigit(c)){s=s*10+(c^48);c=getchar();}
    return s*base;
}
ll a[2047][2047],rj[2047],b[2047][2047];
ll n,m,xmin,xmax;
ll check(ll w){
    rj[0]=m;
    for(ll i=1;i<=n;++i){
        for(rj[i]=0;rj[i]<rj[i-1]&&a[i][rj[i]+1]<=xmin+w;++rj[i]);
        for(ll j=rj[i]+1;j<=m;++j)if(a[i][j]<xmax-w)return 0;
    }
    return 1;
}
void rrotate(){
    for(ll i=1;i<=n;++i)for(ll j=1;j<=m;++j)b[j][n-i+1]=a[i][j];
    swap(n,m);
    for(ll i=1;i<=n;++i)for(ll j=1;j<=m;++j)a[i][j]=b[i][j];
}
int main(){
#ifdef cnyali_lk
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
#endif
    n=read();
    m=read();
    xmin=0x3f3f3f3f3f3f3f3f,xmax=0xcccccccccccccccc;
    for(ll i=1;i<=n;++i)for(ll j=1;j<=m;++j){a[i][j]=read();chkmin(xmin,a[i][j]);chkmax(xmax,a[i][j]);}
    ll ans=0x3f3f3f3f3f3f3f3f,l,r,mid;
    for(ll i=0;i<4;++i){
        l=0;
        r=ans-1;
        while(l<=r){
            mid=(l+r)>>1;
            if(check(mid))r=mid-1;
            else l=mid+1;
        }
        ans=r+1;
        rrotate();
    }
    printf("%lld\n",ans);
    
    return 0;
}

C

先考虑给定$a_i$无修改的情况。

欧拉定理：当$b\ge \varphi(p)$时，$a^b=a^{b\bmod \varphi(p)+\varphi(p)}$

所以可以通过计算$a^b\bmod p+[a^b\ge p]\cdot p$来计算答案。

大概就是：

int query(int l,int r,int p){
    if(l==r)return a[l]%p+(a[l]>=p)*a[l];
    return calc(a[l],query(l+1,r,phi(p)),p);
}

其中$calc(a,b,p)$表示计算$a^b\bmod p+[a^b\ge p]\cdot p$。

正确性显然吧。

但是太慢了。

我们发现，对$p$不断地做$p=\varphi(p)$，很快就会得到1，而1之后就没有必要再算了。

（据说是$O(\log n)$次？）（算出来当$p\le 2\cdot 10^7$时最多24次）

什么？区间修改？差分完直接树状数组维护就好了。

快速幂是$O(\log n)$的，树状数组也可以$O(\log n)$单点查询。

int query(int l,int r,int p){
    if(l==r||p==1)return a[l]%p+(a[l]>=p)*a[l];
    return calc(a[l],query(l+1,r,phi(p)),p);
}

时间复杂度$O(n\log^2 n) $。

浴谷八连测R3 题解

A

B

C

添加新评论

最新文章

最近回复

分类

归档

其它