清华集训2014 奇数国
CTT2014 Day1T3。
但是最水。
ZKW牛逼!
题意
一个长度为100000的序列,起初全为3。
要求支持修改某一个位置上的值,和求出\(\varphi(\)区间积\()\)。
在任何时候,这个数列中每个数都可以表示为\(x=\prod_{i=1}^{60}p_i^{a_i}\)其中\(p_i\)是素数表中第i个素数,例如\(p_1=2,p_2=3,p_3=5\)。
\(a_i\)为非负整数,且\(x\le 10^6\)。
一个非常暴力的复杂度假的算法
由于\(\varphi(x)=\prod_{k_i>0}p_i^{k_i-1}(p_i-1)\)。其中\(x=\prod p_i^{k_i}\)。
我们可以对这60个质数分别计算在区间中的出现次数然后强算。
计算时用树状数组和快速幂,时间复杂度\(O(60 n\log n)\)。
然后似乎卡不掉,但是很慢。
(质数表当然要打表
/*
Author: CNYALI_LK
LANG: C++
PROG: odd.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
#define x first
#define y second
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef long long ll;
typedef pair<int,int> pii;
template<class T>int chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>int chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
int read(){
int s=0,base=1;
char c;
while(!isdigit(c=getchar()))if(c=='-')base=-base;
while(isdigit(c)){s=s*10+(c^48);c=getchar();}
return s*base;
}
const int N=100000,gkk=60;
int BIT[gkk+5][N+10];
void Add(int x,int y,int z){
while(y<=N){
BIT[x][y]+=z;
y+=y&(-y);
}
}
int Sum(int x,int y){
int ans=0;
while(y){
ans+=BIT[x][y];
y^=y&(-y);
}
return ans;
}
int a[N+10][gkk+5];
const int primes[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281};
const ll p=19961993;
ll fpm(ll a,ll b){
ll c=1;
while(b){
if(b&1)c=c*a%p;
a=a*a%p;
b>>=1;
}
return c;
}
int main(){
#ifdef cnyali_lk
freopen("odd.in","r",stdin);
freopen("odd.out","w",stdout);
#endif
int n,x,y;
n=read();
for(int i=1;i<=N;++i){a[i][1]=1;Add(1,i,1);}
for(;n;--n){
if(read()){
x=read();
y=read();
for(int i=0;i<gkk;++i){
int s=0;
while(!(y%primes[i])){++s;y/=primes[i];}
Add(i,x,s-a[x][i]);
a[x][i]=s;
}
}
else{
x=read();y=read();
ll ans=1,s=0;
for(int i=0;i<gkk;++i){
s=Sum(i,y)-Sum(i,x-1);
if(s==0)continue;
ans=ans*(primes[i]-1)%p*fpm(primes[i],s-1)%p;
}
printf("%lld\n",ans);
}
}
return 0;
}
一个非常暴力的复杂度真的算法
由于\(\varphi(x)=x\prod_{k_i>0}\frac{p_i-1}{p_i}\)。其中\(x=\prod p_i^{k_i}\)。
可以计算区间的乘积和有哪些质数在任何一个元素中出现。
前一个直接计算,后一个因为质数个数\(=60\),所以可以通过存long long 然后or运算计算。
都可以用线段树。
就可以\(O(n\log n)\)了。
(\(\frac{p_i-1}{p_i}\)当然也要打表
卡常历程
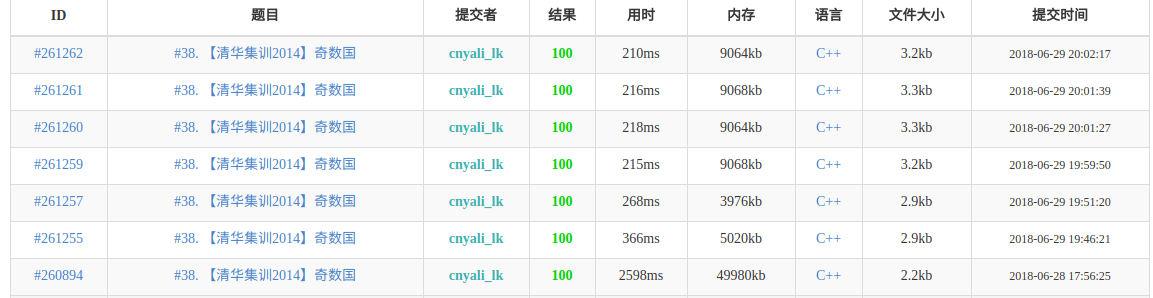
第一次提交是那个复杂度错误的算法。
对lk来说,500000的线段树足以称得上卡常。
虽然这只有100000,但是lk也不想直接写线段树。
yici因为要区间or和,也不能用树状数组。
但是是单点修改区间计算,所以lk选择使用ZKW线段树。
写好以后就是第二次提交。
出现在了第二页的第一个。
似乎有些long long 没有用可以改成int...
然后就得到了第三次提交。
已经比之前的最优解快46ms了。
这么大的读入输出量,也可以加上fread诶...
然后就是第四次到最后一次提交(卡时间计算差异)。
然后就比之前的最优解快了\(\frac{1}{3}\)。
/*
Author: CNYALI_LK
LANG: C++
PROG: odd.cpp
Mail: cnyalilk@vip.qq.com
*/
#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define DEBUG printf("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define Debug debug("Passing [%s] in LINE %d\n",__FUNCTION__,__LINE__)
#define all(x) x.begin(),x.end()
#define x first
#define y second
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
typedef int ll;
typedef pair<ll,ll> pii;
template<class T>ll chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>ll chkmax(T &a,T b){return a<b?a=b,1:0;} template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
const int bufl=1<<22;
char bufi[bufl],*inf=bufi;
char bufo[bufl],*ouf=bufo;
int read(){
int k=0;
while(!isdigit(*inf))++inf;
while(isdigit(*inf)){
k=k*10+(*inf-'0');
++inf;
}
return k;
}
void writeint(int x){
if(x/10)writeint(x/10);
*ouf=x%10+'0';
++ouf;
}
const ll N=131072,gkk=60,M=262144;
const ll primes[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281};
const ll inv[]={9980997,13307996,7984798,11406854,14517814,18426456,9393880,5253157,16490343,8260136,2575742,18343454,3895024,17640832,1698894,3013132,7443456,4581442,9236147,18275065,6562848,2779519,7936697,4037258,6379607,19566707,13566404,4104336,3662752,13602421,16661192,1219054,13259427,9047523,3751248,8196316,14621843,1714528,12192356,11884887,8029406,13455046,17976246,13342473,14084859,15548287,10217514,9846724,5364237,3486812,1627803,14950615,1076789,12406658,19340609,8652728,7791857,7955334,1657495,8808852};
const ll p=19961993;
ll mul[M+233];
long long appear[M+233];
void Change(ll x,ll y){
x+=N;
mul[x]=y;
appear[x]=0;
for(ll i=0;i<60;++i)if(!(y%primes[i]))appear[x]|=(1LL<<i);
for(x>>=1;x;x>>=1){mul[x]=(long long )mul[x<<1]*mul[x<<1|1]%p;appear[x]=appear[x<<1]|appear[x<<1|1];}
}
ll Phi(ll l,ll r){
l+=N;r+=N;
ll prod=1;
long long app=0;
while(l<r){
if(l&1){
prod=(long long )prod*mul[l]%p;
app|=appear[l];
++l;
}
if(!(r&1)){
prod=(long long )prod*mul[r]%p;
app|=appear[r];
--r;
}
l>>=1;r>>=1;
}
if(l==r){prod=(long long )prod*mul[l]%p;app|=appear[l];}
for(ll i=0;i<60;++i)if(app&(1LL<<i))prod=(long long)prod*inv[i]%p;
return prod;
}
int main(){
#ifdef cnyali_lk
freopen("odd.in","r",stdin);
freopen("odd.out","w",stdout);
#endif
fread(bufi,1,bufl,stdin);
ll n,x,y;
n=read();
for(ll i=0;i<100000;++i){mul[i+N]=3;appear[i+N]=2;}
for(ll i=100000;i<N;++i)mul[i+N]=1;
for(ll i=N-1;i;--i){
mul[i]=(long long )mul[i<<1]*mul[i<<1|1]%p;
appear[i]=appear[i<<1]|appear[i<<1|1];
}
for(;n;--n){
if(read()){
x=read()-1;y=read();
Change(x,y);
}
else{
x=read()-1;y=read()-1;
writeint(Phi(x,y));
*ouf='\n';
++ouf;
}
}
fwrite(bufo,1,ouf-bufo,stdout);
return 0;
}